Vissza az előzőleg látogatott oldalra (nem elérhető funkció)

Fogalom megjelenítés (nem elérhető funckió)

Tanulási útmutató

Összefoglalás

Ebben a leckében megismerkedhetünk az ún. „elemi” rendezésekkel, és egy igen hatékonynak mondhatóval is (shell). Mivel a rendezés alapfeladatához sok megoldást adunk, jogosan vethető föl a kérdés, hogy melyik közülük a legjobb. A „legjobbság” egyik kritériuma a hatékonyság, ezért az ezzel kapcsolatos legelemibb fogalmakat is megemlítjük. Ezen fogalmak birtokában jellemezzük az említésre kerülő rendezési algoritmusokat.

Követelmény

Önállóan megoldható feladatok

Fel a lap tetejéreTartalomjegyzék

Rendezések és hatékonyságmérések
- A rendezés specifikációja
- A rendező algoritmusok

Rendezések és hatékonyságmérések

A sorozathoz sorozatot rendelő feladattípusok egyik tagját külön vizsgáljuk ebben a fejezetben.

Az alapfeladat egy N elemű sorozat nagyság szerinti sorba rendezése. A sorozat elemei olyanok, amelyekre a <, ≤ relációk léteznek. Feltesszük a feladatok mindegyikében, hogy a sorozathoz létezik indexelés művelet, és ezt a megoldásban ki is használjuk. Az eredmény a módszerek jelentős részében helyben keletkezik, az eredeti sorrend elvész.

Példa

Konkrét feladatok ismertetése és megoldása helyett itt egy számpéldát fogunk végignézni az egyes rendezési módszerek alkalmazásával. E számsorozat – egy kivétellel – a következő lesz: 5, 3, 9, 1, 7.

A rendezés specifikációja

Bemenet

N:Egész, X:Tömb[1..N:Valami]

Kimenet

X:Tömb[1..N:Valami]

Előfeltétel

N≥0 és RendezettHalmazE(Valami)

Utófeltétel

RendezettE(X’) és X’∈Permutáció(X)

Vissza a tartalomjegyzékhez

A rendező algoritmusok

Az egyes módszereket összehasonlítjuk tárigény (a rendezésben részt vevő tárolóhelyek száma), valamint végrehajtási idő (hasonlítások száma, mozgatások száma) szerint. A helyfoglalásba nem számítjuk bele a ciklusváltozókat, a végrehajtási időbe pedig ezek növelését, vizsgálatát, hiszen ezek mérete és ideje nem függ a rendezendő elemek típusától.

A hasonlítások és a mozgatások száma néha nem függ a rendezendő elemek értékétől, a legtöbb esetben azonban igen, így csak minimális és maximális számukról beszélhetünk. Használni fogjuk az ún. Ordó függvényt, amelynek a matematikában szokásos jelentése a következő: valamilyen jellemző értékét kifejező polinom legmagasabb hatványkitevőjű tagja x-szel arányos. Például: az O(x²) az ’ax² + bx + c’ típusú (paraméteres) függvénycsaládot jelöl.

1. Egyszerű cserés rendezés

Az első módszer a következő ötletre épül. Hasonlítsuk össze az első elemet a sorozat összes többi mögötte levő elemével, és ha valamelyik kisebb nála, akkor cseréljük meg azzal! Így elérhetjük, hogy a sorozat első helyére a legkisebb elem kerüljön. Folytassuk ugyanezen az elven a sorozat második elemével, utoljára pedig az utolsó előttivel!

Rendezés(N,X):

Ciklus I=1-től N-1-ig

Ciklus J=I+1-től N-ig

Ha X[I]>X[J] akkor Csere(X[I],X[J])

Ciklus vége

Eljárás vége.

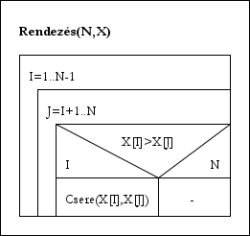Egyszerű cserés rendezés

Példa

A belső ciklus ciklusfeltétele kiértékelése előtt a sorozat:

A futás lépései	A futás értékelése
I=1 ⇒ 5, 3, 9, 1, 7 3, 5, 9, 1, 7 3, 5, 9, 1, 7 1, 5, 9, 3, 7 1, 5, 9, 3, 7 I=2 ⇒ 1, 5, 9, 3, 7 1, 5, 9, 3, 7 1, 3, 9, 5, 7 1, 3, 9, 5, 7 I=3 ⇒ 1, 3, 9, 5, 7 1, 3, 5, 9, 7 1, 3, 5, 9, 7 I=4 ⇒ 1, 3, 5, 9, 7 1, 3, 5, 7, 9	Helyfoglalás: N+1, azaz O(N) Hasonlítások száma: N(N-1)/2, azaz O(N²) Mozgatások száma: 0 – 3N*(N-1)/2, azaz O(N²) [a csere 3 mozgatást kíván]

A futás lépései

A futás értékelése

I=1 ⇒
5, 3, 9, 1, 7
3, 5, 9, 1, 7
3, 5, 9, 1, 7
1, 5, 9, 3, 7
1, 5, 9, 3, 7
I=2 ⇒
1, 5, 9, 3, 7
1, 5, 9, 3, 7
1, 3, 9, 5, 7
1, 3, 9, 5, 7
I=3 ⇒
1, 3, 9, 5, 7
1, 3, 5, 9, 7
1, 3, 5, 9, 7
I=4 ⇒
1, 3, 5, 9, 7
1, 3, 5, 7, 9

Helyfoglalás: N+1, azaz O(N)

Hasonlítások száma: N*(N-1)/2, azaz O(N²)

Mozgatások száma: 0 – 3*N*(N-1)/2, azaz O(N²)

[a csere 3 mozgatást kíván]

Az animáció bemutatja az egyszerű cserés rendezést

Egyszerű cserés rendezés

2. Minimumkiválasztásos rendezés

Az előző – egyszerű – módszer hibája a sok felesleges csere. Célszerűbb lenne az aktuális első elemet a mögötte levők közül egyedül a legkisebbel cserélni. Ehhez a rendező ciklus belsejében cserék helyett egy minimumkiválasztást kell csinálni.

Rendezés(N,X):

Ciklus I=1-től N-1-ig

MIN:=I

Ciklus J=I+1-től N-ig

Ha X[MIN]>X[J] akkor MIN:=J

Ciklus vége

Csere(X[I],X[MIN])

Ciklus vége

Eljárás vége.

A Minimumkiválasztásos rendezés algoritmusa, struktogrammal.

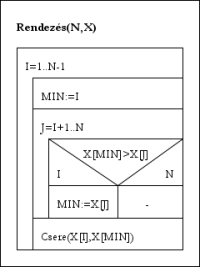Minimukiválasztásos rendezés

Példa

Itt a számpéldát a külső ciklus ciklusfeltételének kiértékelése előtt vizsgáljuk:

A futás lépései	A futás értékelése
I=1 ⇒ 5, 3, 9, 1, 7 I=2 ⇒ 1, 3, 9, 5, 7 I=3 ⇒ 1, 3, 9, 5, 7 I=4 ⇒ 1, 3, 5, 9, 7	Helyfoglalás: N+1, azaz O(N) Hasonlítások száma: N(N-1)/2, azaz O(N²) Mozgatások száma: 3(N-1)/2, azaz O(N)

A futás lépései

A futás értékelése

I=1 ⇒

5, 3, 9, 1, 7

I=2 ⇒

1, 3, 9, 5, 7

I=3 ⇒

1, 3, 9, 5, 7

I=4 ⇒

1, 3, 5, 9, 7

Helyfoglalás: N+1, azaz O(N)

Hasonlítások száma: N*(N-1)/2, azaz O(N²)

Mozgatások száma: 3*(N-1)/2, azaz O(N)

Megjegyzés

Érdekessége a módszernek az, hogy a mozgatások száma szerencsétlen esetben rosszabb lehet, mint az előzőé, amelynek javításaként keletkezett. Ez amiatt van, hogy itt a külső ciklusban mindenképpen cserélünk. Meg lehetne ugyan vizsgálni, hogy érdemes-e cserélni, de ez a vizsgálat a legtöbb esetben növelné a futási időt.

Az animáció bemutatja a minimumkiválasztásos rendezést

Minimumkiválasztásos rendezés

3. Buborékos rendezés

Most egy másik rendezési alapelvet vizsgálunk meg: hasonlítsuk egymással a szomszédos elemeket, és ha a sorrendjük nem jó, akkor cseréljük meg őket!

Ezzel a módszerrel egy cikluslépés lefutása alatt a legnagyobb elem biztosan a sorozat végére kerül, és ezen kívül a nagyobb értékű elemek hátrafelé, a kisebbek pedig előrefelé mozdulnak el (innen van a buborékmódszer elnevezés).

Rendezés(N,X):

Ciklus I=N-től 2-ig -1-esével

Ciklus J=1-től I-1-ig

Ha X[J]>X[J+1] akkor Csere(X[J],X[J+1])

Ciklus vége

Eljárás vége.

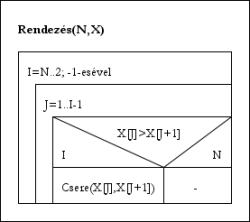Buborékos rendezés

Példa

Újra a belső ciklusnál nézzük a konkrét rendezési példát:

A futás lépései	A futás értékelése
I=5 ⇒ 5, 3, 9, 1, 7 3, 5, 9, 1, 7 3, 5, 9, 1, 7 3, 5, 1, 9, 7 3, 5, 1, 7, 9 I=4 ⇒ 3, 5, 1, 7, 9 3, 5, 1, 7, 9 3, 1, 5, 7, 9 3, 1, 5, 7, 9 I=3 ⇒ 3, 1, 5, 7, 9 1, 3, 5, 7, 9 1, 3, 5, 7, 9 I=2 ⇒ 1, 3, 5, 7, 9 1, 3, 5, 7, 9	Helyfoglalás: N+1, azaz O(N) Hasonlítások száma: N(N-1)/2, azaz O(N²) Mozgatások száma: 0 – 3N*(N-1)/2, azaz O(N²) [a csere 3 mozgatást kíván]

A futás lépései

A futás értékelése

I=5 ⇒

5, 3, 9, 1, 7
3, 5, 9, 1, 7
3, 5, 9, 1, 7
3, 5, 1, 9, 7
3, 5, 1, 7, 9

I=4 ⇒
3, 5, 1, 7, 9
3, 5, 1, 7, 9
3, 1, 5, 7, 9
3, 1, 5, 7, 9
I=3 ⇒
3, 1, 5, 7, 9
1, 3, 5, 7, 9
1, 3, 5, 7, 9
I=2 ⇒
1, 3, 5, 7, 9
1, 3, 5, 7, 9

Helyfoglalás: N+1, azaz O(N)

Hasonlítások száma: N*(N-1)/2, azaz O(N²)

Mozgatások száma: 0 – 3*N*(N-1)/2, azaz O(N²)

[a csere 3 mozgatást kíván]

Az animáció bemutatja a buborékos rendezést

Buborékos rendezés

Megállapíthatjuk, hogy várakozásunk ellenére a hatékonysági jellemzők egyáltalán nem javultak.

4. Javított buborékos rendezés

Az előző módszer azért nem váltotta be reményeinket, mert nem használtuk ki benne, hogy az elemek a helyük felé elmozdultak. A legegyszerűbb esetben, például ha a belső ciklus egy lefutása alatt egyáltalán nem volt csere, akkor felesleges minden további hasonlítás, a rendezéssel készen vagyunk. Ha volt csere, de például a legutolsó a sorozat közepénél volt, akkor ebből tudhatjuk, hogy a sorozat a közepe után biztosan kész, rendezett, és csak az előtte levő résszel kell foglalkozni.

Figyeljük tehát minden menetben a legutolsó csere helyét, és a következő menetben csak addig rendezzünk! (Át kell térni „amíg”-os ciklusra.)

Rendezés(N,X):

I:=N

Ciklus amíg I≥2

CS:=0

Ciklus J=1-től I-1-ig

Ha X[J]>X[J+1] akkor Csere(X[J],X[J+1]); CS:=J

Ciklus vége

I:=CS

Ciklus vége

Eljárás vége.

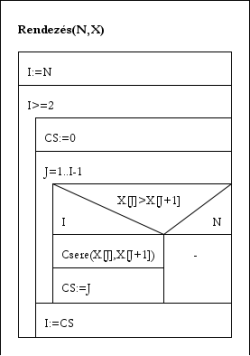Javított buborékos rendezés

Példa

Az előző módszer számpéldájából sorok maradnak ki:

A futás lépései	A futás értékelése
I=5 ⇒ 5, 3, 9, 1, 7 3, 5, 9, 1, 7 3, 5, 9, 1, 7 3, 5, 1, 9, 7 3, 5, 1, 7, 9 I=4 ⇒ 3, 5, 1, 7, 9 3, 5, 1, 7, 9 3, 1, 5, 7, 9 3, 1, 5, 7, 9 I=2 ⇒ 1, 3, 5, 7, 9 1, 3, 5, 7, 9	Helyfoglalás: N+1, azaz O(N) Hasonlítások száma: N-1 – N(N-1)/2, azaz O(N²) Mozgatások száma: 0 – 3N*(N-1)/2, azaz O(N²) [a csere 3 mozgatást kíván]

A futás lépései

A futás értékelése

I=5 ⇒

5, 3, 9, 1, 7
3, 5, 9, 1, 7
3, 5, 9, 1, 7
3, 5, 1, 9, 7
3, 5, 1, 7, 9

I=4 ⇒
3, 5, 1, 7, 9
3, 5, 1, 7, 9
3, 1, 5, 7, 9
3, 1, 5, 7, 9
I=2 ⇒
1, 3, 5, 7, 9
1, 3, 5, 7, 9

Helyfoglalás: N+1, azaz O(N)

Hasonlítások száma: N-1 – N*(N-1)/2, azaz O(N²)

Mozgatások száma: 0 – 3*N*(N-1)/2, azaz O(N²)

[a csere 3 mozgatást kíván]

Az animáció bemutatja a javított buborékos rendezést

Javított buborékos rendezés

A hasonlítások számában javulást látunk, az igazi javulás azonban nem a minimális és a maximális, hanem az átlagos végrehajtási időben van.

5. Beillesztéses rendezés

Újabb rendezési elvvel ismerkedünk meg. Az eddigi módszerek mindegyike olyan volt, hogy a sorozatot felosztotta egy már kész, rendezett szakaszra, és a rendezést a másik szakasz elemei között folytatta. Másik jellemzőjük volt, hogy a rendezés elkezdéséhez már az összes elemnek rendelkezésre kellett állnia.

Most a kártyakeveréshez hasonló elvből indulunk ki: egyetlen elem mindig rendezett; ha van egy rendezett részsorozatunk, akkor abba a nagyság szerinti helyére illesszük be a soron következő elemet!

Rendezés(N,X):

Ciklus I=2-től N-ig

J:=I-1

Ciklus amíg J>0 és X[J]>X[J+1]

Csere(X[J],X[J+1]); J:=J-1

Ciklus vége

Eljárás vége.

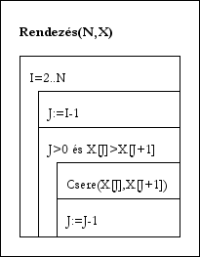Beillesztéses rendezés

Példa

A számpélda a belső ciklus feltételénél itt a következőképpen alakul:

A futás lépései	A futás értékelése
I=2 ⇒ 5, 3, 9, 1, 7 3, 5, 9, 1, 7 I=3 ⇒ 3, 5, 9, 1, 7 I=4 ⇒ 3, 5, 9, 1, 7 3, 5, 1, 9, 7 3, 1, 5, 9, 7 1, 3, 5, 9, 7 I=5 ⇒ 1, 3, 5, 9, 7 1, 3, 5, 7, 9	Helyfoglalás: N+1, azaz O(N) Hasonlítások száma: N-1 – N(N-1)/2, azaz O(N²) Mozgatások száma: 0 – 3N*(N-1)/2, azaz O(N²) [a csere 3 mozgatást kíván]

A futás lépései

A futás értékelése

I=2 ⇒

5, 3, 9, 1, 7
3, 5, 9, 1, 7

I=3 ⇒
3, 5, 9, 1, 7

I=4 ⇒

3, 5, 9, 1, 7
3, 5, 1, 9, 7
3, 1, 5, 9, 7
1, 3, 5, 9, 7

I=5 ⇒
1, 3, 5, 9, 7
1, 3, 5, 7, 9

Helyfoglalás: N+1, azaz O(N)

Hasonlítások száma: N-1 – N*(N-1)/2, azaz O(N²)

Mozgatások száma: 0 – 3*N*(N-1)/2, azaz O(N²)

[a csere 3 mozgatást kíván]

Az animáció bemutatja a beillesztéses rendezést

Beillesztéses rendezés

6. Javított beillesztéses rendezés

Észrevehetjük az előző módszernél, hogy a beillesztő ciklusban a legtöbb elem egyszer mozdul el, a beillesztendő viszont sokszor. Ezt a sok mozgást is csökkenthetjük egyetlenegyre úgy, hogy a beillesztendőt nem tesszük azonnal be a sorozatba, hanem csak a többieket tologatjuk hátra, és a beillesztendőt csak a végén tesszük a helyére.

Rendezés(N,X):

Ciklus I=2-től N-ig

J:=I-1; Y:=X[I]

Ciklus amíg J>0 és X[J]>Y

X[J+1]:=X[J]; J:=J-1

Ciklus vége

X[J+1]:=Y

Ciklus vége

Eljárás vége.

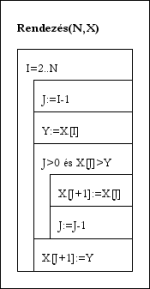Javított beillesztéses rendezés

Példa

Az elemek mozgatása miatt ebben a példában a kivett elem visszahelyezéséig egyes elemek kétszer szerepelnek.

A futás lépései	A futás értékelése
I=2 ⇒ 5, 3, 9, 1, 7 5, 5, 9, 1, 7 I=3 ⇒ 3, 5, 9, 1, 7 I=4 ⇒ 3, 5, 9, 1, 7 3, 5, 1, 9, 7 3, 1, 5, 9, 7 3, 3, 5, 9, 7 I=5 ⇒ 1, 3, 5, 9, 7 1, 3, 5, 7, 9	Helyfoglalás: N+1, azaz O(N) Hasonlítások száma: N-1 – N(N-1)/2, azaz O(N²) Mozgatások száma: 2(N-1) – 2(N-1)+N(N-1)/2, azaz O(N²)

A futás lépései

A futás értékelése

I=2 ⇒

5, 3, 9, 1, 7
5, 5, 9, 1, 7

I=3 ⇒
3, 5, 9, 1, 7

I=4 ⇒

3, 5, 9, 1, 7
3, 5, 1, 9, 7
3, 1, 5, 9, 7
3, 3, 5, 9, 7

I=5 ⇒
1, 3, 5, 9, 7
1, 3, 5, 7, 9

Helyfoglalás: N+1, azaz O(N)

Hasonlítások száma: N-1 – N*(N-1)/2, azaz O(N²)

Mozgatások száma: 2*(N-1) – 2*(N-1)+N*(N-1)/2, azaz O(N²)

Az animáció bemutatja a javított beillesztéses rendezést

Javított beillesztéses rendezés

7. Szétosztó rendezés

A három alaprendezés és azok javításai után speciális rendezésekkel foglalkozunk, amelyekben előfeltételként speciális megszorításaink lesznek.

A legelsőben feltesszük, hogy a rendezendő elemek olyan rekordok, amelyek kulcsmezője (vagy egy abból kiszámolt számérték) 1 és N közötti természetes szám lehet, s nincs két azonos kulcsú rekord.

A kulcsmező itt egyértelműen megadja azt a helyet, ahova az elemet tenni kell, így semmi hasonlításra nincs szükség. A módszerhez azonban egy újabb tömbre van szükség, ahova az eredményt elhelyezzük.

A specifikáció

Bemenet

N:Egész, X:Tömb[1..N:Valami], Valami=(kulcs,egyéb)

Kimenet

Y:Tömb[1..N:Valami]

Előfeltétel

N≥0 és X.kulcs∈Permutáció((1,...,N))

Utófeltétel

RendezettE(Y.kulcs) és Y∈Permutáció(X)

Az algoritmus

Rendezés(N,X,Y):

Ciklus I=1-től N-ig

Y(X[I].kulcs):=X[I]

Ciklus vége

Eljárás vége.

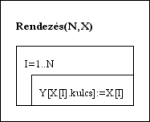Szétosztó rendezés

Megjegyzés

Itt a speciális feltétel miatt meg kell változtatnunk a példasorozatot: 3, 2, 5, 1, 4 (most csak a kulcsmező értékét tároljuk). A feladat másik specialitása miatt pedig két sorozatot kell adnunk: a bemenetet és az eredményt. Az eredmény még nem kitöltött tagjait is jelöljük: ∅.

Példa

Be-/Kimenet	A futás lépései	A futás értékelése
Bemenet	3, 2, 5, 1, 4
Kimenet	I=1 ⇒ ∅, ∅, ∅, ∅, ∅ I=2 ⇒ ∅, ∅, 3, ∅, ∅ I=3 ⇒ ∅, 2, 3, ∅, ∅ I=4 ⇒ ∅, 2, 3, ∅, 5 I=5 ⇒ 1, 2, 3, ∅, 5 I=6 ⇒ 1, 2, 3, 4, 5	Helyfoglalás: 2N, azaz O(N) Hasonlítások száma: 0, azaz O(0) Mozgatások száma: N, azaz O(N) Kulcsmező-indexelések száma*: N, azaz O(N)

Be-/Kimenet

A futás lépései

A futás értékelése

Bemenet

3, 2, 5, 1, 4

Kimenet

I=1 ⇒
∅, ∅, ∅, ∅, ∅

I=2 ⇒
∅, ∅, 3, ∅, ∅

I=3 ⇒
∅, 2, 3, ∅, ∅

I=4 ⇒
∅, 2, 3, ∅, 5

I=5 ⇒

1, 2, 3, ∅, 5

I=6 ⇒

1, 2, 3, 4, 5

Helyfoglalás: 2*N, azaz O(N)

Hasonlítások száma: 0, azaz O(0)

Mozgatások száma: N, azaz O(N)

Kulcsmező-indexelések száma: N, azaz O(N)

Az animáció bemutatja a szétosztó rendezést

Szétosztó rendezés

8. Számlálva szétosztó rendezés

Egy kicsit kevesebbet követel előfeltételként a következő rendezés: itt az elemek kulcsmezője lehet az [1,N]-nél szélesebb intervallumban is, és nem szükséges feltétel a kulcsok különbözősége sem.

A specifikáció

Bemenet

N,M:Egész, X:Tömb[1..N:Valami], Valami=(kulcs,egyéb)

Kimenet

Y:Tömb[1..N:Valami]

Előfeltétel

N≥0 és M≥0 és ∀i(1≤i≤N): X[i].kulcs∈{1..M}

Utófeltétel

RendezettE(Y.kulcs) és Y∈Permutáció(X)

Az algoritmus

Itt első lépésként számoljuk le minden lehetséges kulcsértékre, hogy hány ilyen értékű elem van! Mivel a kulcsértékekkel indexelhetünk, ezért a számlálás egyetlen indexeléssel elvégezhető minden elemre.

Másodjára minden lehetséges kulcsértékhez határozzuk meg a nála kisebb vagy egyenlő kulcsú rekordok számát!

Harmadik lépésként minden elemet közvetlenül a helyére helyezhetünk a fenti információ alapján.

Rendezés(N,X,M):

Db[1..M]:=0

Ciklus I=1-től N-ig

Db[X[I].kulcs]:=Db[X[I].kulcs]+1

Ciklus vége

Ciklus J=2-től M-ig

Db[J]:=Db[J]+Db[J-1]

Ciklus vége

Ciklus I=1-től N-ig

Y[Db[X[I].kulcs]]:=X[I]

Db[X[I].kulcs]:= Db[X[I].kulcs]-1

Ciklus vége

Eljárás vége.

Számlálva szétosztó rendezés

Megjegyzés

Itt a speciális rendezés miatt újabb példasorozatot vizsgálunk: 5, 3, 5, 1, 7. A bemenet mellett először a Db vektor értékeit közöljük, majd az eredményt.

Példa

Bemenet	Db
5, 3, 5, 1, 7	I=1 ⇒ 0, 0, 0, 0, 0, 0, 0 I=2 ⇒ 0, 0, 0, 0, 1, 0, 0 I=3 ⇒ 0, 0, 1, 0, 1, 0, 0 I=4 ⇒ 0, 0, 1, 0, 2, 0, 0 I=5 ⇒ 1, 0, 1, 0, 2, 0, 0 I=6 ⇒ 1, 0, 1, 0, 2, 0, 1

Bemenet

5, 3, 5, 1, 7

I=1 ⇒

0, 0, 0, 0, 0, 0, 0

I=2 ⇒

0, 0, 0, 0, 1, 0, 0

I=3 ⇒

0, 0, 1, 0, 1, 0, 0

I=4 ⇒

0, 0, 1, 0, 2, 0, 0

I=5 ⇒

1, 0, 1, 0, 2, 0, 0

I=6 ⇒

1, 0, 1, 0, 2, 0, 1

A második ciklusban:

Db	Kimenet	A futás értékelése
J=2 ⇒ 1, 0, 1, 0, 2, 0, 1 J=3 ⇒ 1, 1, 1, 0, 2, 0, 1 J=4 ⇒ 1, 1, 2, 0, 2, 0, 1 J=5 ⇒ 1, 1, 2, 2, 2, 0, 1 J=6 ⇒ 1, 1, 2, 2, 4, 0, 1 J=7 ⇒ 1, 1, 2, 2, 4, 4, 1 1, 1, 2, 2, 4, 4, 5	I=1 ⇒ ∅, ∅, ∅, ∅, ∅ I=2 ⇒ ∅, ∅, ∅, 5, ∅ I=3 ⇒ ∅, 3, ∅, 5, ∅ I=4 ⇒ ∅, 3, 5, 5, ∅ I=5 ⇒ 1, 3, 5, 5, ∅ I=6 ⇒ 1, 3, 5, 5, 7	Helyfoglalás: 2N+Me, azaz O(N+M) Hasonlítások száma: 0, azaz O(0) Mozgatások száma: N, azaz O(N) Kulcsmező-indexelések száma: 5*N, azaz O(N)

Kimenet

A futás értékelése

J=2 ⇒

1, 0, 1, 0, 2, 0, 1

J=3 ⇒

1, 1, 1, 0, 2, 0, 1

J=4 ⇒

1, 1, 2, 0, 2, 0, 1

J=5 ⇒

1, 1, 2, 2, 2, 0, 1

J=6 ⇒

1, 1, 2, 2, 4, 0, 1

J=7 ⇒

1, 1, 2, 2, 4, 4, 1

1, 1, 2, 2, 4, 4, 5

I=1 ⇒

∅, ∅, ∅, ∅, ∅

I=2 ⇒

∅, ∅, ∅, 5, ∅

I=3 ⇒

∅, 3, ∅, 5, ∅

I=4 ⇒

∅, 3, 5, 5, ∅

I=5 ⇒

1, 3, 5, 5, ∅

I=6 ⇒

1, 3, 5, 5, 7

Helyfoglalás: 2*N+M*e, azaz O(N+M)

Hasonlítások száma: 0, azaz O(0)

Mozgatások száma: N, azaz O(N)

Kulcsmező-indexelések száma: 5*N, azaz O(N)

Az animáció bemutatja a számlálva szétosztó rendezést

Számlálva szétosztó rendezés

9. Számláló rendezés

Az egyszerű cserés módszer mozgatásainak számát is javíthatjuk az egyik újabb módszer, a szétosztó rendezés segítségével. A cserés rendezésnél ne cserélgessük az elemeket, hanem csak számoljuk meg mindegyikre, hogy hány nála kisebb, illetve az őt megelőzők között hány vele egyenlő van (magát is beleértve). Ezzel a rendezendő adatsorhoz a [0,N-1] intervallum egész számainak egy permutációját rendeltük. Ez a permutáció lehet a bemenete a szétosztó rendezésnek.

Rendezés(N,X):

Db[1..N]:=1 [a tömb 1-es értékekkel feltöltése]

Ciklus I=1-től N-1-ig

Ciklus J=I+1-től N-ig

Ha X[I]>X[J] akkor Db[I]:=Db[I]+1

különben Db[J]:=Db[J]+1

Ciklus vége

Ciklus I=1-től N-ig

Y[Db[I]]:=X[I] [szétosztó rendezés]

Ciklus vége

Eljárás vége.

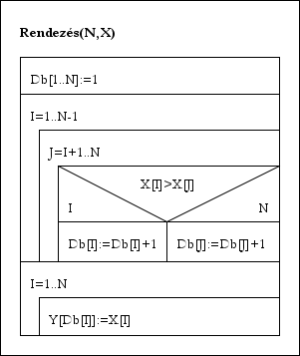Számláló rendezés

Példa

Újra az eredeti (5, 3, 9, 1, 7) számsorozatot vizsgáljuk:

Db	Kimenet	A futás értékelése
I=1 ⇒ 1, 1, 1, 1, 1 2, 1, 1, 1, 1 2, 1, 2, 1, 1 3, 1, 2, 1, 1 3, 1, 2, 1, 2 I=2 ⇒ 3, 1, 2, 1, 2 3, 1, 3, 1, 2 3, 2, 3, 1, 2 3, 2, 3, 1, 3 I=3 ⇒ 3, 2, 3, 1, 3 3, 2, 4, 1, 3 3, 2, 5, 1, 3 I=4 ⇒ 3, 2, 5, 1, 3 3, 2, 5, 1, 4	I=1 ⇒ ∅, ∅, ∅, ∅, ∅ I=2 ⇒ ∅, ∅, 5, ∅, ∅ I=3 ⇒ ∅, 3, 5, ∅, ∅ I=4 ⇒ ∅, 3, 5, ∅, 9 I=5 ⇒ 1, 3, 5, ∅, 9 I=6 ⇒ 1, 3, 5, 7, 9	Helyfoglalás: 2N+N, azaz O(N) Hasonlítások száma: N(N-1)/2, azaz O(N²) Mozgatások száma:* N, azaz O(N) 2-szeres indexelés: N, azaz O(N)

Kimenet

A futás értékelése

I=1 ⇒

1, 1, 1, 1, 1
2, 1, 1, 1, 1
2, 1, 2, 1, 1
3, 1, 2, 1, 1
3, 1, 2, 1, 2
I=2 ⇒

3, 1, 2, 1, 2
3, 1, 3, 1, 2
3, 2, 3, 1, 2
3, 2, 3, 1, 3
I=3 ⇒

3, 2, 3, 1, 3
3, 2, 4, 1, 3
3, 2, 5, 1, 3
I=4 ⇒

3, 2, 5, 1, 3
3, 2, 5, 1, 4

I=1 ⇒

∅, ∅, ∅, ∅, ∅
I=2 ⇒

∅, ∅, 5, ∅, ∅
I=3 ⇒

∅, 3, 5, ∅, ∅
I=4 ⇒

∅, 3, 5, ∅, 9
I=5 ⇒

1, 3, 5, ∅, 9
I=6 ⇒

1, 3, 5, 7, 9

Helyfoglalás: 2*N+N*, azaz O(N)

Hasonlítások száma: N*(N-1)/2, azaz O(N²)

Mozgatások száma: N, azaz O(N)

2-szeres indexelés: N, azaz O(N)

Az animáció bemutatja a rendezési algoritmusok elvét:

Az animáció bemutatja a számlálva szétosztó rendezést

Számlálva szétosztó rendezés

10. Rendezés shell-módszerrel

Sokat javíthat a rendező módszeren, ha először a nagy távolságú elemeket hasonlítjuk és cseréljük, mert így az egyes elemek nagyon gyorsan közel kerülhetnek a végleges helyükhöz. Ha egy rendezés ezt az információt kihasználja, akkor az eredetinél lényegesen jobbat kaphatunk. Ilyen módszer például a beillesztéses rendezés.

A használt lépésköz többféle lehet. Közös jellemzőjük, hogy szigorúan monoton csökkenők, és utoljára éppen 1 az értékük.

Példa

Például rendezzük az alábbi 15 elemű sorozatot!

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.	14.	15.
15	4	30	8	12	7	1	-6	25	5	-10	2	19	41	2

Legyen a kezdő lépésköz 4, tehát a következő részsorozatokat kell rendezni:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.	14.	15.
15				12				25				19

	4				7				5				41

		30				1				-10				2

			8				-6				2

Ezeket külön-külön rendezzük:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.	14.	15.
12				15				19				25

	4				5				7				41

		-10				1				2				30

			-6				2				8

A 4-esével rendezett vektor a következő:

1.	2.	3.	4.	5.	6.	7.	8.	9.	10.	11.	12.	13.	14.	15.
12	4	-10	-6	15	5	1	2	19	7	2	8	25	41	30

Ezután felezzük a lépésközt, kettesével rendezzük a sorozatot, végül pedig egyesével! A módszer előnye azonnal látszik: viszonylag kevés művelettel „nagyjából” rendezett lesz a vektor, a kicsi számok előre kerülnek, a nagyok pedig hátra, és egyre felezve a lépésközt, már csak kisebb korrekciókat kell végrehajtani a sorrendben.

Rendezés(N,X):

L:=L0

Ciklus amíg L≥1 [lépésköz-ciklus]

Ciklus K=L+1-től 2*L-ig [K: az L. részsorozat 2. eleme]

Ciklus I=K-tól N-ig L-esével

J:=I-L; Y:=X[I] [javított beillesztéses rendezés]

Ciklus amíg J>0 és X[J]>Y

X[J+L]:=X[J]; J:=J-L

Ciklus vége

X[J+L]:=Y

Ciklus vége

L:=Következő(L)

Ciklus vége

Eljárás vége.

Shell rendezés

Az L értékének meghatározására többféle módszer van. Lehetséges, hogy 2^k-1 alakú, lehetséges, hogy Fibonacci-szám alakú. Kezdőértékként mindenképpen olyan értéket kell meghatározni, amelyik nem lépi túl az N értékét, majd a Következő függvény így alakul:

Következő(L): [2^k-1 alakú esetben]

Következő:=(L+1)/2-1

Függvény vége.

.. és a másik:

Következő(L): [Fibonacci-szám alakú esetben]

L2:=L-L1; L:=L1; L1:=L2; Következő:=L1

Függvény vége.

Megjegyzés

Ha L1 és L egymás utáni Fibonacci-számok, akkor L2 az előző Fibonacci-szám lesz. A módszernél nyilván előre adott az L0 (kezdő L) és az L1 értéke.

Az animáció bemutatja a rendezések összehasonlítását:

Rendezések összehasonlítása

Az animáció bemutatja a táblázatkezelő program használatát a hatékonyságvizsgálatban, amelyet a rendezések vizsgálatánál is felhasználhatunk:

Hatékonyságvizsgálat táblázatkezelővel

Vissza a tartalomjegyzékhez