Alapvető adatmodellezési ismeretek; program-Excel tábla export-import
Ebben a leckében a központi fogalom a rendezés, a rendezettség lesz. Azt vizsgáljuk, hogy miként használható ki egy sorozat rendezettsége az algoritmus hatékonyságnövelése érdekében. A táblázatkezelő lesz segítségünkre abban, hogy a „mért” eredményekből kényelmesen vonhassunk le következtetéseket.
1. Keresés rendezett sorozatban
Ebben az esetben adott egy rendezett sorozat, amelyben egy adott értékű elem sorszámát kell meghatározni, ha az benne van a sorozatban.
A specifikáció
Bemenet
N:Egész, X:Tömb[1..N:Valami], Y:Valami, T:Valami→Logikai
Kimenet
VAN:Logikai, SORSZ:Egész
Előfeltétel
N≥0 és RendezettE(X)
Utófeltétel
VAN = (∃i (1≤i≤N): X[i]=Y) és
VAN → 1≤SORSZ≤N és X[SORSZ]=Y
Az algoritmus
Próbáljuk először a lineáris keresést alkalmazni e feladat megoldására! A feladat specialitásából következik, hogy ha egy, a keresett elemnél nagyobb értékű elemet találunk, akkor a keresett elem már biztosan nem fordulhat elő, a keresést be lehet fejezni. Emiatt a program utófeltétele a következő lesz:
Utófeltétel
VAN = (∃i (1≤i≤N): X[i]=Y) és
VAN → 1≤SORSZ≤N és X[SORSZ]=Y és ∀i(1≤i<SORSZ): X[i]<Y
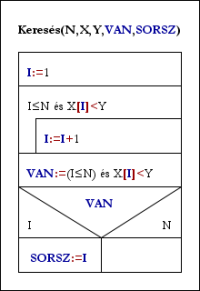
Keresés(N,X,Y,VAN,SORSZ):
I:=1
Ciklus amíg I≤N és X[I]<Y
I:=I+1
Ciklus vége
VAN:=(I≤N) és X[I]=Y
Ha VAN akkor SORSZ:=I
Eljárás vége.
Nézzük meg, hogy e keresést milyen hasonlításszám jellemez!
- Minimum: 1,
- Átlag: (N+1)/2,
- Maximum: N
Az átlagos hasonlításszámban szereplő lineáris összefüggés miatt hívják e keresést lineáris keresésnek.
2. Keresés rendezett tömbben
A rendezettséget (és az indexelhetőséget) másképpen is kihasználhatjuk. Vizsgáljuk meg első lépésben a sorozat középső elemét! Ha ez a keresett elem, akkor készen vagyunk. Ha a keresett elem ennél kisebb, akkor csak az ezt megelőzőek között lehet, tehát a keresést a továbbiakban a sorozatnak erre a részére kell alkalmazni. Ha a keresett elem ennél nagyobb, akkor pedig ugyanezen elv alapján a sorozat ezt követő részére.
A megoldás szintén az utófeltételt módosítja, szigorítja. Itt az előzővel ellentétben nem lehet tudni, hogy a megtalált érték az azonos értékűek közül az első, az utolsó vagy pedig valamelyik középső lesz.
A specifikáció
Utófeltétel
VAN = (∃i (1≤i≤N): X[i]=Y) és
VAN → 1≤SORSZ≤N és X[SORSZ]=Y és ∀i(1≤i<SORSZ): X[i]≤Y és ∀i(SORSZ<i≤N): X[i]≥Y
Az algoritmus
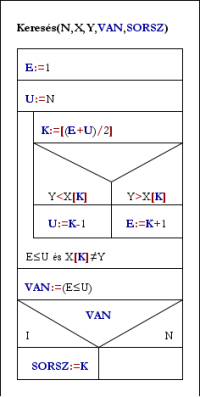
Keresés(N,X,Y,VAN,SORSZ):
E:=1; U:=N
Ciklus
K:=[(E+U)/2] [E+U felének egész értéke]
Elágazás
Y<X[K] esetén U:=K-1
Y>X[K] esetén E:=K+1
Elágazás vége
Ciklus amíg E≤U és Y≠X[K]
VAN:=E≤U
Ha VAN akkor SORSZ:=K
A hasonlításszám:
- Minimum: 1,
- Átlag: log2(N),
- Maximum: log2(N)+1
Az átlagos hasonlítás-számban szereplő logaritmikus összefüggés miatt hívják e keresést logaritmikus keresésnek, illetve a sorozat felezésére utalva felezéses vagy bináris keresésnek.
Ennek a keresésnek is meg lehet alkotni a rokonait, mint azt tettük a lineáris kereséssel, azaz készíthetünk belőle eldöntést, kiválasztást, megszámolást, kiválogatást. Ezek közül nézzük meg a kiválogatást!
A kiválogatás módosított specifikációja
Bemenet
N:Egész, X:Tömb[1..N:Valami], Y:Valami, T:Valami→Logikai
Kimenet
VAN:Logikai, E,U:Egész
Előfeltétel
N≥0 és RendezettE(X)
Utófeltétel
VAN = (∃i (1≤i≤N): X[i]=Y) és
VAN → 1≤E≤U≤N és ∀i(E≤i≤U): X[i]=Y és ∀i(i<E): X[i]<Y és ∀i(U<i): X[i]>Y
Nyilvánvaló, hogy az azonos értékű elemek itt mindenképpen egymás mellett fognak szerepelni, azaz a kiválogatáshoz elég megadni az első, illetve az utolsó ilyen elem sorszámát. Ezt úgy tesszük meg, hogy a logaritmikus keresés után előre, illetve hátrafelé megkeressük az utolsó megfelelő elemet.
A kiválogatás módosított algoritmusa
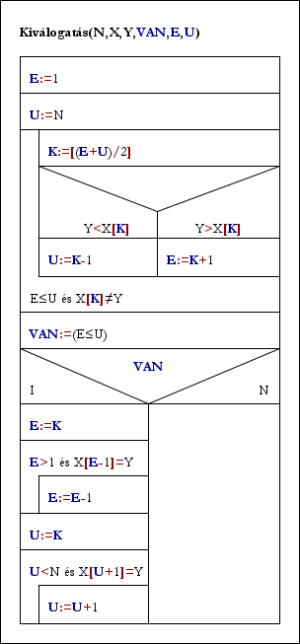
Kiválogatás(N,X,Y,VAN,E,U):
E:=1; U:=N
Ciklus
K:=[(E+U)/2]
Elágazás
Y<X[K] esetén U:=K-1
Y>X[K] esetén E:=K+1
Elágazás vége
amíg E≤U és X[K]≠Y
Ciklus vége
VAN:=(E≤U)
Ha VAN akkor E:=K
Ciklus amíg E>1 és X[E-1]=Y
E:=E-1
Ciklus vége
U:=K
Ciklus amíg U<N és X[U+1]=Y
U:=U+1
Ciklus vége
Elágazás vége
Eljárás vége.
3. Összefuttatás – rendezettek uniója
Bizonyos esetekben az unió feladattípus megoldása az előző fejezetbelinél hatékonyabb lehet.
Folytatva a korábbi „hagyományt” ezt is konkrét feladatokon keresztül vizsgáljuk.
F35. Egy osztály lány-, illetve fiútanulóinak névsora alapján állítsuk elő az osztálynévsort!
F36. Egy iskolában négy szakkörre járnak tanulók (van aki többre is). A szakkörnévsorok alapján állítsuk elő a szakkörre járó tanulók névsorát!
Megállapíthatjuk, hogy az általános egyesítéshez képest itt az a specialitás, hogy mindegyik sorozatként ábrázolt halmaz rendezett, s az eredménynek is rendezettnek kell lenni.
Ha nem két sorozatról van szó, akkor az a korábbiaknak megfelelően visszavezethető két sorozat feldolgozására.
A specifikáció
Bemenet
N,M:Egész, X:Tömb[1..N:Valami], Y:Tömb[1..M:Valami]
Kimenet
Db:Egész, Z:Tömb[1..N+M:Valami]
Előfeltétel
N≥0 és M≥0 és HalmazE(X) és HalmazE(Y) és
RendezettE(X) és RendezettE(Y)
Utófeltétel
Db=N + SZUM(i=1..M; Y[i] ∉X) 1 és
∀ i(1 ≤ i ≤ Db) : (Z[i] ∈ X vagy Z[i] ∈ Y)
és HalmazE(Z) és RendezettE(Z)
Az algoritmus
A megoldásban haladjunk párhuzamosan a két sorozatban! Az eredmény első eleme vagy X[1] vagy Y[1] lesz. Amelyik kisebb, azt az eredménysorozatba tesszük, abban a sorozatban kell továbblépni egy elemmel, s újra egy-egy elemet hasonlítani. Ha egyenlők voltak, akkor az egyiket másoljuk az eredménybe, majd mindkét sorozatban továbblépünk. Ha az egyiknek a végére értünk, akkor a másikat minden változtatás nélkül az eredménybe másoljuk.
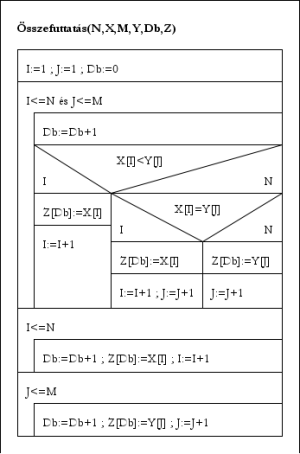
Összefuttatás(N,X,M,Y,Db,Z):
I:=1; J:=1; Db:=0
Ciklus amíg I≤N és J≤M
Db:=Db+1
Elágazás
X[I]<Y[J] esetén Z[Db]:= X[I]; I:=I+1
X[I]=Y[J] esetén Z[Db]:= X[I]; I:=I+1; J:=J+1
X[I]>Y[J] esetén Z[Db]:=Y[J]; J:=J+1
Elágazás vége
Ciklus vége
Ciklus amíg I≤N
Db:=Db+1; Z[Db]:=X[I]; I:=I+1
Ciklus vége
Ciklus amíg J≤M
Db:=Db+1; Z[Db]:=Y[J]; J:=J+1
Ciklus vége
Eljárás vége.
Észrevehetjük a megoldást elemezve, hogy ha olyan szerencsénk volt, hogy X[N]=Y[M], akkor az utolsó két ciklusra tulajdonképpen nincs is szükség, hiszen nem maradt másolnivaló. Az a baj, hogy ez a szerencsés eset viszonylag ritkán fordul elő.
A második megoldásváltozatban mi magunk idézzük elő e szerencsét: mindkét sorozat végére egy nagyon nagy (az adott típus legnagyobb értéke), de egyező elemet teszünk.
Összefuttatás(N,X,M,Y,Db,Z):
I:=1; J:=1; Db:=0
X[N+1]:=+ ∞; Y[M+1]:=+ ∞ [az elemtípus maximális értéke]
Ciklus amíg I<N+1 vagy J<M+1
Db:=Db+1
Elágazás
X[I]<Y[J] esetén Z[Db]:=X[I]; I:=I+1
X[I]=Y[J] esetén Z[Db]:=X[I]; I:=I+1; J:=J+1
X[I]>Y[J] esetén Z[Db]:=Y[J]; J:=J+1
Elágazás vége
Ciklus vége
Eljárás vége.
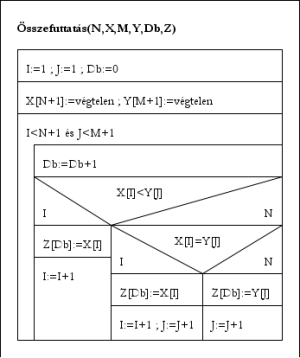
Ebben a megoldásban a hozzávett fiktív elem nem kerül be az eredménybe. Ha szükségünk lenne rá, a ciklus vége után még elhelyezhetnénk az eredmény végére.
A harmadik változatban kihasználjuk azt a – nem minden feladatban meglevő – specialitást, hogy a két sorozatban biztosan nincs közös elem. Ilyen például az F35. feladat. Ezt az altípust a megkülönböztetés érdekében összefésülésnek nevezzük.
Összefésülés(N,X,M,Y,Db,Z):
I:=1; J:=1; Db:=0
X[N+1]:=+∞; Y[M+1]:=+∞ [az elemtípus maximális értéke]
Ciklus amíg I<N+1 vagy J<M+1
Db:=Db+1
Ha X[I]<Y[J] akkor Z[Db]:=X[I]; I:=I+1
különben Z[Db]:=Y[J]; J:=J+1
Ciklus vége
Eljárás vége.
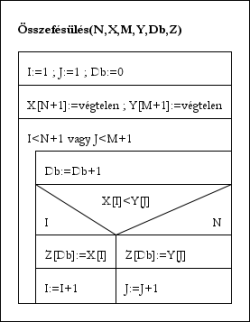
Az animáció bemutatja néhány tétel speciális változatát, amely rendezett elemekre vonatkozik:
4. Hatékonysági megfontolások
Az alábbi feladatok azt firtatják, miként készíthető „helyben” hatékony algoritmus a jól ismert alapvető problémákra amellett a feltétel mellett, hogy „helyben”, vagy „kettő helyett egyetlen sorozatban” kell az eredményt előállítani.
Kiválogatás helyben
Adott egy sorozat. Hagyjuk meg a bemeneti sorozatban a T tulajdonságúakat és csak azokat!
Bemenet
N:Egész, X:Tömb[1..N:Valami]
Kimenet
Db:Egész, X’:Tömb[1..N:Valami]
Előfeltétel
N≥0
Utófeltétel
Db = SZUM(i=1..N;T(X[i])) 1 és
X’[1..Db] ⊆ X és
∀ i (1 ≤ i ≤ Db) : T(X’[i])
Az X’ – szokás szerint – az X kimenetkori értékét jelöli.
Gondolja meg az algoritmusát!
Szétválogatás helyben
Adott egy sorozat. Válogassuk úgy szét a T- és a nem T-tulajdonságú elemeit, hogy egyetlen sorozatot alkosson a két sorozat!
Segítségképpen megadjuk a specifikációt:
Bemenet
N:Egész, X:Tömb[1..N:Valami]
Kimenet
Db:Egész, X’:Tömb[1..N:Valami]
Előfeltétel
N≥0
Utófeltétel
Db= SZUM (i=1..N;T(X[i])) 1 és X’ ∈ Permutáció(X)
és ∀ i (1 ≤ i ≤ Db) : T(X’[i])
és ∀ i (Db+1 ≤ i ≤ N): nem T(X’[i])
Az X’ –szokás szerint– az X kimenetkori értékét jelöli.
Gondolja meg az algoritmusát!
Hatékonyságvizsgálat táblázatkezelővel
A kiinduló ötlet a táblázatkezelők alábbi szolgáltatásaira építenek:
- A táblázatkezelők képesek importálni Comma Separated Value (CSV-) formátumú fájlt.
- A CSV egy „mezei” text fájl, amelyben minden önálló adatot pontosvessző követ; a táblázat minden sorát a fájlban sorvégjel zár le.
- Egyszerű olyan C++ programot írni, amely a táblázatolandó adatokat „CSV-esítve” írja egy text fájlba.
Példafeladatként oldjuk meg az unió és az összefuttatás tételek hatékonyságának összevetését! A hatékonyság szempontja legyen a tömbbeli elemek összehasonlítás-száma.
Megoldásvázlat:
- Mindkét algoritmusban számoljuk a tömbelem-összehasonlításokat.
- Néhány (jól kiválasztott, esetleg az összes) (N,M)-elemű sorozatra sokszor lefuttatjuk, közben számláljuk a hasonlításokat (majd átlagoljuk); és CSV-fájlba írjuk az eredményeket. (N az X-, M az Y-sorozat elemeinek a számát jelöli.)
Vegyük észre, hogy lényegében egy összegzés tételbe kell ágyaznunk valamely tételt (jelen esetben először az uniót, másodikként az összefuttatást), aminek a végrehajtása közben valaminek (jelen esetben az összehasonlítások) számát számláljuk.
Hogy a létrehozandó táblázatról (=a generálandó eredményfájlról) kellő elképzelésünk legyen, lássunk egy mintát!
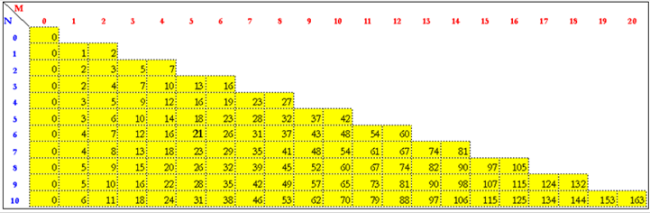A táblázat az unió tétel hasonlítás-számát mutatja a két sorozat elemszámának a függvényében.A „száraz” numerikus (átlag) eredményeket hisztogrammá alakítva könnyebben elemezhetőbbé tehetjük az alábbi, tendenciákat jól mutató diagrammal. Így jutunk az alábbi ábrához:
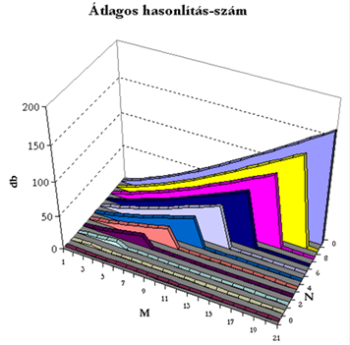A felületdiagram az unió tétel hasonlítás-számát mutatja a két sorozat elemszámának a függvényében.Ha a fenti vizsgálatot elvégezzük az összefutatásra is, akkor a következőket kapjuk:
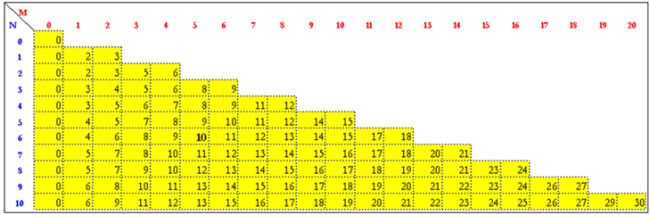A táblázat az összefuttatás tétel hasonlítás-számát mutatja a két sorozat elemszámának a függvényében.... és a tendenciára:
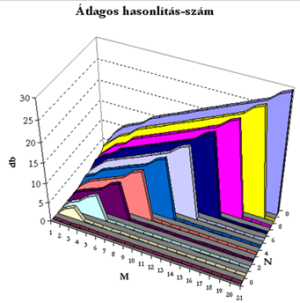A felületdiagram az összefuttatás tétel hasonlítás-számát mutatja a két sorozat elemszámának a függvényében.Annyi egész biztosan első ránézésre is látszik, hogy az unió „működése” négyzetes hatékonyságú, amíg az összefutatás nagyjából lineáris. A konklúzió tehát az, hogy a méretparaméterekkel növekedve az összefuttatás határozottan jobban teljesít, hiszen az összehasonlítás-számban egyre jobban „alulmarad” a konkurens, unió tételhez képest.
Az animáció bemutatja azt, hogy a hatékonysági kérdések – az elemek helyben hagyása – hogyan módosíthatja az algoritmusokat.
