Tanulási útmutató
Összefoglalás
Ebben a leckében szóba kerülnek a ciklusok különféle formái, adatszerkezeti oldalról a párjának tekinthető tömbök.
Követelmény
Önállóan megoldható feladatok
{esszé}
Fogalmazza meg saját szavaival: mit tartalmaz a specifikáció negyedik, utófeltétel nevű része!
{/esszé}
Ciklusok, tömbök; adatszerkezet-programszerkezet
Még emlékezünk egy korábbi leckében látható alábbi ábrára, amely „madártávlatból” összefoglalja az egyes adatszerkezet kategóriák (skalár, sokaság …) és az őket feldolgozó algoritmikus szerkezetek (transzformáció, ciklus …) kapcsolatát.
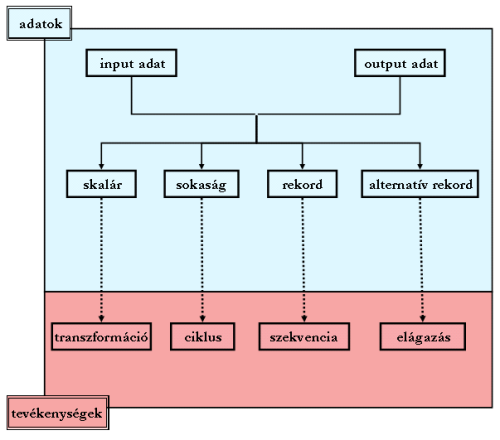Adatok, tevékenységek és kapcsolatuk.Ebben a leckében figyeljünk föl erre a kapcsolatra a tömb (az elsőként elénk kerülő összetett adatszerkezet) és a ciklus megismerése közben!
1. Iterált típusok
Iteráltnak nevezik az a típust, amely egy típus iterálásával (azaz tetszőleges számú ismétlésével) kapható meg. Egyszerűbben mondva: olyan összetett típusról van szó, amelyhez olyan értékek tartoznak, amely mindegyike felbontható valahány, azonos típusba sorolható „elemre”. Az iterált típusok egyike a tömb. Erről szólunk az alábbiakban. További fontos iterált típusokkal is fogunk találkozni, így a szövegtípussal, a szövegfájl típusokkal.
1.1. Tömb-típuskonstrukció
Az elemi adatszerkezetekkel foglalkozó leckénkben alkalmazott rövid leírást követjük a tömb fogalmának, lényegének leírásánál. Azaz megadjuk az általa létrejövő típus értékhalmazát és a vele kapcsolatba hozható műveletek, relációk felsorolását. Ezt kibővítjük – a már nem nélkülözhető – definiálás szintaxisának a leírásával. (Ezt hívjuk itt és a későbbiekben is strukturálásnak.)
Strukturálás
Tömbtípus = Tömb[Indextípus : Értéktípus]
Értékhalmaz
az alaphalmaz „indexterjedelem-szeres” hatványa (indexterjedelemnyi Értéktípus elemek „egyesített” halmaza).
Műveletek
szelekciós függvény, amellyel az egyes elemek kiválaszthatók: [.] ahol a . egy Indextípusú kifejezést jelöl.
Relációk
= (tömbelemenkénti összehasonlítás, egyezőség), ≠.
Konstans n : Egész=99
Típus Elem = Valós
Vektor = Tömb[1..n : Elem]
Változó v : Vektor
i : 1..n
…
Be: v
Ciklus i=2-től n-1-ig
Ha T(v[i]) akkor v[I]:=(v[i-1]+v[i+1])/2
Ciklus vége
… és egy másik:
Konstans HóHosszak = Tömb[1..12 : Egész]=(31,28,31,30,31,30,31,31,30,31,30,31)
Változó h,n : Egész
i : 1..n
dik : Egész
…
Be: h,n
dik:=0
Ciklus i=1-től h-1-ig
dik:=dik+HóHosszak[i]
Ciklus vége
dik:=dik+n
Az animációban példákon keresztül kerül megvilágításra a tömb fogalma, használata:
2. Ciklusok
Alapvető algoritmikus struktúra a ciklus. A tömör lényege: utasítások megismétlése többször. Már tudjuk, a ciklusnak többféle fajtája van. Nézzük ezeket sorra!
2.1. Feltételes ciklusok
Ciklus amíg logikai kifejezés
utasítássorok
Ciklus vége
Az első lehetőség az ismétlést egy feltételhez kötni: amíg a logikai kifejezés (az ún. ciklusfeltétel) igaz értékű, addig a ciklus belsejében szereplő utasításokat (az ún. ciklusmagot) végre kell hajtani. Ha a logikai kifejezés már hamis értékű, akkor a Ciklus vége utáni utasításnál kell folytatni a végrehajtást.
A felírás formájából is látszik, hogy itt a ciklusfeltételt a ciklusmag végrehajtása előtt kell kiértékelni (ezt hívják elöltesztelő ciklusnak), és elképzelhető, hogy a ciklusmagot egyszer sem hajtjuk végre.
I:=2
Ciklus amíg I≤N és I † N [†: nem osztható]
I:=I+1
Ciklus vége
A ciklusfeltételt nemcsak a ciklusmag előtt, hanem mögötte is elhelyezhetjük. Ez lesz az ún. hátultesztelő ciklus.
Ciklus
utasítássorok
amíg logikai kifejezés
Ciklus vége
Ugyanúgy, mint az elöltesztelő ciklusnál, itt is akkor fejezzük be a végrehajtást, ha a logikai kifejezés hamis értékű, és akkor kezdjük elölről a ciklusmagot, ha igaz.
I:=0
Ciklus
I:=I+1; Ki: NÉV[I]
amíg NÉV[I]≠"KISS ANNA"
Ciklus vége
Sok programozási nyelvben létezik e ciklusnak olyan változata, ahol nem a bennmaradás, hanem a kilépés feltételét kell a hátultesztelős ciklushoz megfogalmazni, tehát az itt megfogalmazottnak épp az ellenkezőjét.
Ez a ciklus olyan, hogy a ciklusmagját egyszer mindenképpen végrehajtjuk, és csak utána vizsgáljuk, hogy kell-e még, vagy sem.
2.2. Számlálós ciklusok
Az elöltesztelős ciklusnak van egy speciális változata, amelyet külön is megvizsgálunk, először egy példával.
Össze kell adnunk egy számsorozat elemeit: az elsőt, a másodikat, … utoljára az N.-t.
amíg-os változat | ↔ | számlálós változat |
|---|---|---|
I:=1; S:=0 Ciklus amíg I≤N S:=S+A[I]; I:=I+1 Ciklus vége | ↔ | S:=0 Ciklus I=1-től N-ig S:=S+A[I] Ciklus vége |
Az olyan elöltesztelős ciklusokat nevezzük számlálós ciklusnak, amelyekben egy változó adott intervallumon belüli összes értékére végre kell hajtanunk a ciklusmagot. Az elöltesztelő jellegből következik, hogy ha az intervallum üres, akkor a ciklusmagot egyszer sem hajtjuk végre.
Egyes programozási nyelvek, illetve azok egyes implementációi a számlálós ciklust hátultesztelősként definiálják, emiatt használatával üres intervallum esetén óvatosan kell bánnunk.
Ciklus cv=K-tól V-ig
utasítássorok
Ciklus vége
Az ilyen ciklusban a cv változó (az ún. ciklusváltozó) először felveszi a K (kezdő)értéket. Ha ez V (vég)értéknél kisebb, akkor végrehajtjuk a ciklusmagot, majd K értékét növeljük a [K..V] intervallum következő elemére, és újra vizsgáljuk a végrehajtás feltételét. Ha a ciklusváltozó túllépi a végértéket, akkor a Ciklus vége utáni utasításnál kell folytatni a végrehajtást.
A számlálós ciklus ciklusváltozója tetszőleges olyan változó lehet, amelynél van értelme következő értékről beszélni, pl.:
Ciklus BETŰ='A'-tól 'Z'-ig
Ki: BETŰ
Ciklus vége
Egyes esetekben a számlálós ciklust nem kell az intervallum minden elemére végrehajtani, hanem csak minden valahányadikra, illetve nem növekvő, hanem csökkenő sorrendben kell haladni. Ezekre az esetekre szolgál a számlálós ciklus második változata.
Ciklus cv=K-tól V-ig L-esével
utasítássorok
Ciklus vége
Annyi a különbség az első változathoz képest, hogy a ciklusmag végrehajtása után a ciklusváltozó nem a következő értéket veszi fel, hanem értéke az előző értékhez képest L-lel nő (azaz csökken, ha L negatív volt).
Ciklus X=-p-től p-ig 0.01-osával
Ki: X,sin(X)
Ciklus vége
(Ekkor a következést a lépésköz egyértelműsíti.)
Az animációban feladatokon keresztül figyelhetjük meg az egyes ciklusfajták használatát:
Végezetül figyelmébe ajánljuk a következő dokumentumot:
- Fájl letöltése: A C++ alapelemeihez olvassa el a dokumentum 6-8., 11-13. oldalait! című háttéranyag letöltése
- Információ az állományról: A dokumentumban szó kerül a következőkre: elágazások, ciklusok, tömbök.
- Fájlméret: 0.37 MB
