Tanulási útmutató
Összefoglalás
A tananyag vége felé közeledve kitekintünk a továbblépési lehetőségekre. Olyan feladatokat nézünk át, amelyek alapvetően más tantárgyak témakörébe tartoznak, de a Programozási alapismeretek tantárgy eszközkészletével tökéletesen megoldhatóak.
Ebben a leckében olyan speciális keresési feladattal foglalkozunk, ahol N db sorozatban kell keresnünk egy-egy értéket úgy, hogy azok egymásnak valamilyen szempont szerint megfeleljenek.
Követelmény
A lecke végére a hallgatónak ismernie kell a visszalépéses keresés filozófiáját, meg kell értenie és el kell tudnia magyarázni az algoritmusát, illetve ezt önállóan is elő kell tudnia állítani. Az ehhez kapcsolódó feladatokban fel kell ismerni, hogy visszalépéses kereséssel oldható meg, és a megoldást elő kell tudni állítani.
Önállóan megoldható feladatok
Visszalépéses keresés (backtrack)
Az alapprobléma és megoldása
Újra konkrét feladatokkal kezdjük e feladattípus ismertetését.
F37. Helyezzünk el egy sakktáblán 8 vezért úgy, hogy egyik se üsse a másikat!
F38. Egy vállalat N db munkára szeretne munkásokat felvenni. Jelentkezik N db munkás, mindegyik megmondja, hogy milyen munkát tudna elvégezni. Osszuk el közöttük a munkákat úgy, hogy mindenkinek jusson munka, s minden munkát elvégezzenek!
F39. N db közért M db pékségtől rendelhet kenyeret. Ismerjük a közértek kenyérigényét, a pékségek sütési kapacitását, valamint azt, hogy melyik közért mely pékségekkel áll kapcsolatban. Adjuk meg, hogy melyik közért melyik pékségtől rendelje a kenyeret, ha mindegyik csak egyetlentől rendelhet!
E feladatok közös jellemzője, hogy eredményük egy sorozat. E sorozat minden egyes tagját valamilyen sorozatból kell kikeresni, de az egyes keresések összefüggenek egymással (vezért nem lehet oda tenni, ahol egy korábban letett vezér ütné; egy munkát nem lehet két munkásnak adni; ha egy pékségnek elfogyott a kenyere, akkor attól már nem lehet rendelni).
Bemenet
N:Egész, M:Tömb[1..N:Egész],
∀i(1≤i≤N): S[i]:Tömb[1..M[i]:Valami],
fk:Egész x Valami x Valami*→Logikai,
ft:Egész x Valami→Logikai
Kimenet
VAN:Logikai, X:Tömb[1..N:Egész]
Előfeltétel
N≥0 és
∀X∈Tömb[1..N:Egész]:
fk(i,S[i][X[i]];S[1][X[1]]...S[i-1][X[i-1]]) →
∀j<i: fk(j,S[j][X[j]];...)
Utófeltétel
VAN ≡ ∃Y∈Tömb[1..N:Egész]: Megoldás(Y) és
VAN → Megoldás(X)
Definíció
Megoldás(X)=(∀i (1≤i≤N): 1≤X[i]≤M[i] és
∀i (1≤i≤N): fk(i,S[i][X[i]];S[1][X[1]],...,S[i-1][X[i-1]]) és
ft(i,S[i][X[i]]))
A fenti definíciót szavakkal megfogalmazva: az X akkor megoldás, ha minden X[i] önmagában helyes, valamint az összes őt megelőző X-beli elem szerint is helyes.
Megállapíthatjuk tehát, hogy minden egyes új választás az összes korábbitól függhet (ezt formalizálja az fk függvény), a későbbiektől azonban nem! Egyes esetekben nemcsak a korábbiaktól, hanem saját jellemzőjétől is függhet a választás (ezt írja le az ft függvény).
Egyes speciális esetekben a korábbiaktól függés a korábbi elemekre külön-külön megvizsgálható (F37, F38), ekkor az előfeltétel triviálisan igaz:
Bemenet
N:Egész, M:Tömb[1..N:Egész],
∀i(1≤i≤N): S[i]:Tömb[1..M[i]:Valami],
fk:Egész x Valami x Egész x Valami → Logikai,
ft:Egész x Valami → Logikai
Kimenet
VAN:Logikai, X:Tömb[1..N:Egész]
Előfeltétel
N≥0
Utófeltétel
VAN ≡ ∃Y∈Tömb[1..N:Egész]: Megoldás(Y) és
VAN → Megoldás(X)
Definíció
Megoldás(X)=(∀i (1≤i≤N): 1≤X[i]≤M[i] és
∀i,j (1≤j<i≤N): fk(i,S[i][X[i]],j,S[j][X[j]]) és
ft(i,S[i][X[i]]))
A megoldás legfelső szintjén keressünk az I. sorozatból megfelelő elemet! Ha ez sikerült, akkor lépjünk tovább az I+1. sorozatra, ha pedig nem sikerült, akkor lépjünk vissza az I-1.-re, s keressünk abban újabb lehetséges elemet!
A keresés befejeződik, ha mindegyik sorozatból sikerült elemet választanunk (I>N) vagy pedig a visszalépések miatt már az elsőből sem tudunk újabbat választani (I<1).
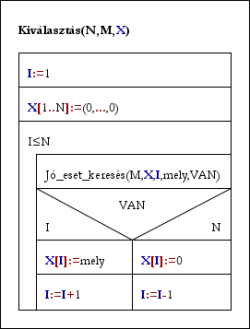
Keresés(N,M,X,VAN):
I:=1; X[1..N]:=(0,...,0)
Ciklus amíg I≥1 és I≤N
Jó_eset_keresés(M,X,I,melyik,VAN)
Ha VAN akkor X[I]:=melyik; I:=I+1 [előrelép]
különben X[I]:=0; I:=I-1 [visszalép]
Ciklus vége
VAN:=(I≥1)
Eljárás vége.
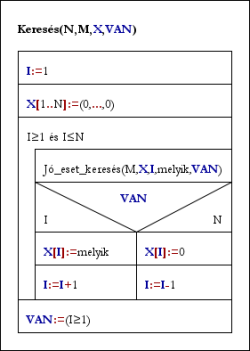
Egy lineáris keresés kezdődik az I. sorozatban:
Jó_eset_keresés(M,X,I,mely,VAN):
mely:=X[I]+1
Ciklus amíg mely≤M[I] és
(Rossz_eset(I,X,mely) vagy nem ft(I,mely))
mely:=mely+1
Ciklus vége
VAN:=(mely≤M[I])
Eljárás vége.

A Rossz_eset függvény az általános esetben a feladattól függő fk függvény kiszámolását jelenti, a fenti speciális esetben pedig egy eldöntést. Ez utóbbit nézzük meg!
Rossz_eset(I,X,mely):
J:=1
Ciklus amíg J<I és fk(I,mely,J,X(J))
J:=J+1
Ciklus vége
Rossz_eset:=(J<I)
Eljárás vége.

Programozási tételek backtrack-es változatai
Az alábbiakban meggondoljuk, hogy miként lehet a fenti keresés tételpárjainak (eldöntés, kiválasztás stb.) backtrack-es változatait megkonstruálni. A fenti megoldást könnyen átalakíthatjuk eldöntéssé, kiválasztássá, megszámolássá, valamint kiválogatássá. Az első kettő a legfelső szint minimális átalakítását igényli, a megszámolást a kiválogatás felhasználja, így ez utóbbit fogalmazzuk meg.
Bemenet
N:Egész, M:Tömb[1..N:Egész],
∀i(1≤i≤N): S[i]:Tömb[1..M[i]:Valami],
fk:Egész x Valami x Egész x Valami → Logikai,
ft:Egész x Valami → Logikai
Kimenet
DB:Egész, Y:(Tömb[1..N:Egész])*
Előfeltétel
N≥0
Utófeltétel
DB=a megoldások számának szokásos megfogalmazása
és ∀j(1≤j≤DB): Megoldás(Y[j]) és HalmazE(Y)
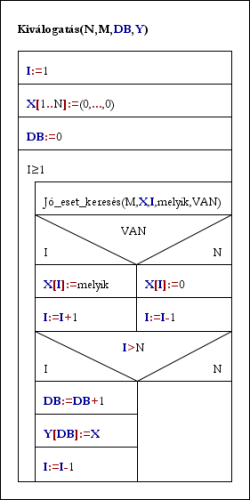
A kiválogatás alapgondolata: ha egy megoldást megtaláltunk, akkor azt írjuk ki, majd lépjünk vissza, mintha ez nem is lenne megoldás.
Kiválogatás(N,M,DB,Y):
I:=1; X[1..N]:=(0,...,0); DB:=0
Ciklus amíg I≥1
Jó_eset_keresés(M,X,I,melyik,VAN)
Ha VAN akkor X[I]:=melyik; I:=I+1 [előrelép]
különben X[I]:=0; I:=I-1 [visszalép]
Ha I>N akkor DB:=DB+1; Y[DB]:=X; I:=I-1
Ciklus vége
Eljárás vége.
A legtöbb esetben nagyon sok megoldást kapunk, így a kiválogatást általában nem kigyűjtéssel, hanem kiírással végezzük. Van azonban egy eset, amelyben tartósabban szükség lehet az eredményekre: ez a minimumkeresés.
Ebben a feladatban a valamilyen szempontból legjobb megoldást kell megadnunk. Megadunk egy kt költségfüggvényt, ami alapján az egyes megoldásokat összehasonlíthatjuk.
Bemenet
N:Egész, M:Tömb[1..N:Egész],
∀i(1≤i≤N): S[i]:Tömb[1..M[i]:Valami],
fk:Egész x Valami x Egész x Valami → Logikai,
ft:Egész x Valami → Logikai
kt:Valami* → Egész
Kimenet
VAN:Logikai, Y:(Tömb[1..N:Egész])*
Előfeltétel
N≥0
Utófeltétel
VAN ≡ ∃Y∈Tömb[1..N:Egész]: Megoldás(Y) és
VAN → (Megoldás(X) és ∀Y:Megoldás(Y) → kt(Y)≥kt(X))
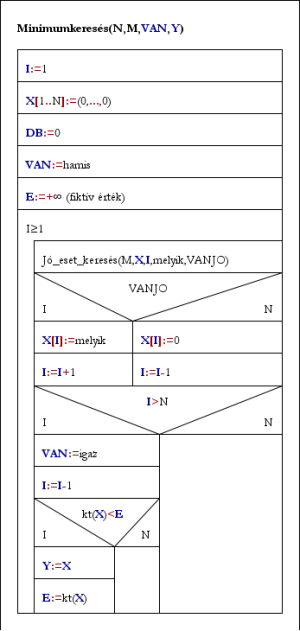
Az algoritmusban a kiválogatásra alapozva állítsunk elő egy megoldást, ezt hasonlítsuk össze az eddigi legjobb megoldással, s ha jobb nála, akkor ezt őrizzük meg! Kiinduló pontnak vegyünk egy fiktív kezdőértéket, amely minden lehetséges megoldásnál biztosan rosszabb!
Minimumkeresés(N,M,VAN,Y):
I:=1; X[1..N]:=(0,...,0); DB:=0
VAN:=hamis; E:=+Ľ [fiktív érték]
Ciklus amíg I≥1
Jó_eset_keresés(M,X,I,melyik,VANJO)
Ha VANJO akkor X[I]:=melyik; I:=I+1 [előrelép]
különben X[I]:=0; I:=I-1 [visszalép]
Ha I>N akkor VAN:=igaz; I:=I-1
Ha kt(X)<E akkor Y:=X; E:=kt(X)
Ciklus vége
Eljárás vége.
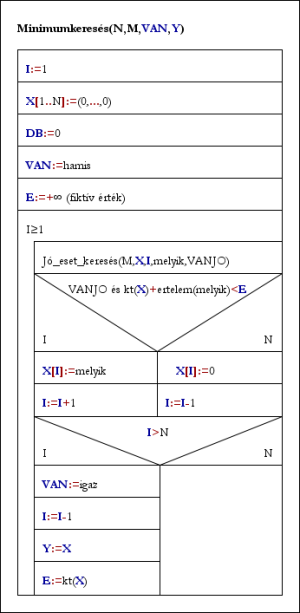
A visszalépéses minimumkeresés hatékonyabb lehet abban a speciális esetben, ha a költségfüggvényt az egyes elemekre vett elemibb értékfüggvényei összegeként (feltéve, hogy ezek nemnegatív értékek) kell kiszámolni, azaz ha:
kt(X)=SZUM(i=1..N) ertelem(X[i])
Ekkor ugyanis a teljes megoldás elkészülte előtt is felfedezhetjük, hogy az éppen készülő megoldás lehet-e még jobb az eddigi legjobbnál.
Minimumkeresés(N,M,VAN,Y):
I:=1; X[1..N]:=(0,...,0); DB:=0
VAN:=hamis; E:=+Ľ [fiktív érték]
Ciklus amíg I≥1
Jó_eset_keresés(M,X,I,melyik,VANJO)
Ha VANJO és kt(X)+ertelem(melyik)<E
akkor X[I]:=melyik; I:=I+1
különben X[I]:=0; I:=I-1
Ha I>N akkor VAN:=igaz; I:=I-1; Y:=X; E:=kt(X)
Ciklus vége
Eljárás vége.
A visszalépéses keresés egy másik változatában nem rögzített elemszámú az eredmény. Egy lehetséges esetben meg kell adni minden olyan (korlátozott elemszámú) sorozatot, amelyet egy nem megfelelő elem zár le.
Definíció
Megoldás(X)=∃K (1≤K≤N):(∀i (1≤i≤K): 1≤X[i]≤M[i]
és ∀i,j (1≤j<i≤N): fk(i,S[i][X[i]],j,S[j][X[j]]) és ft(i,S[i][X[i]])
és (∃j (1≤j<K≤N): fk(K,S[K][X[i]],j,S[j][X[j]]) vagy ft(K,S[K][X[K]])))
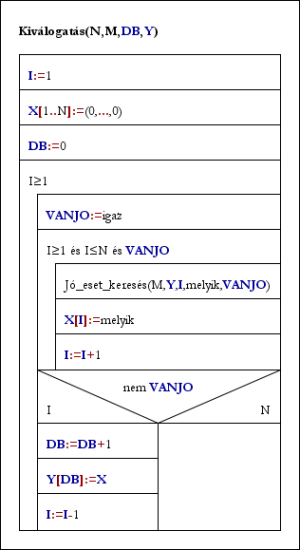
Alakítsuk át a korábban szerepelt kiválogatási algoritmust úgy, hogy a belső ciklus álljon le, ha vissza kellene lépni! Ekkor jegyezzük fel az aktuális állást, lépjünk vissza, majd folytassuk a keresést!
Kiválogatás(N,M,DB,Y):
I:=1; X[1..N]:=(0,...,0); DB:=0
Ciklus amíg I≥1
VANJO:=igaz
Ciklus amíg I≥1 és I≤N és VANJO
Jó_eset_keresés(M,Y,I,melyik,VANJO)
X[I]:=melyik; I:=I+1
Ciklus vége
Ha nem VANJO akkor DB:=DB+1; Y[DB]:=X; I:=I-1
Ciklus vége
Eljárás vége.
Itt is megvizsgálhatnánk a legjobb megoldás algoritmusát, de ezt az előző minimumkereséshez való hasonlósága miatt az Olvasóra hagyjuk.
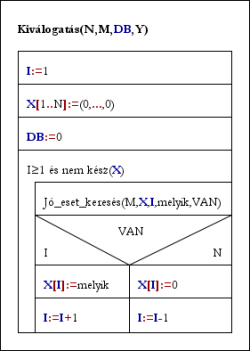
Egy másik lehetséges esetben nem tudjuk, hogy az eredmény hány elemű, csupán azt, hogy mikor van készen. Ezt a kész(X) logikai értékű függvény adja meg.
Kiválogatás(N,M,DB,Y):
I:=1; X[1..N]:=(0,...,0); DB:=0
Ciklus amíg I≥1 és nem kész(X)
Jó_eset_keresés(M,X,I,melyik,VAN)
Ha VAN akkor X[I]:=melyik; I:=I+1 [előrelép]
különben X[I]:=0; I:=I-1 [visszalép]
Ciklus vége
Eljárás vége.
Visszalépéses kereséssel megoldható feladatok
Nézzük meg a fejezet elején közölt feladatok megoldását!
F37. 8 vezér a sakktáblán
F37. Helyezzünk el egy sakktáblán 8 vezért úgy, hogy egyik se üsse a másikat!
Oszloponként egy-egy vezért helyezünk el, a sakktáblán 8 oszlop, oszloponként 8 sor van. Bármelyik két vezér akkor van helyesen elhelyezve, ha nincsenek azonos sorban vagy azonos átlóban.
N=8 a sorozatok száma,
M[i]=N mindegyik sorozat elemszáma egyforma
ft(a,b) = igaz azonosan igaz függvény (a vezér önmagában bárhova tehető)
fk(i,j,k,l) = nem (j=l vagy |i-k|=|j-l|)
A keresés legfelső szintje változatlan, a két további eljárást kell újrafogalmazni.
Jó_eset_keresés(M,X,I,mely,VAN):
mely:=X[I]+1
Ciklus amíg mely≤M[I] és Rossz_eset(I,X,mely)
mely:=mely+1
Ciklus vége
VAN:=(mely≤M[I])
Eljárás vége.
Rossz_eset(I,X,mely):
J:=1
Ciklus amíg J<I és nem(mely=X[J] vagy I-J=|mely-X[J]|)
J:=J+1
Ciklus vége
Rossz_eset:=(J<I)
Eljárás vége.


F38. N ember – N munka
F38. Egy vállalat N db munkára szeretne munkásokat felvenni. Jelentkezik N db munkás, mindegyik megmondja, hogy milyen munkát tudna elvégezni. Osszuk el közöttük a munkákat úgy, hogy mindenkinek jusson munka, s minden munkát elvégezzenek!
A megoldást két változatban készítjük el. Az elsőben az egyes emberek által végezhető munkákat egy-egy sorozatban tároljuk.
N az emberek és az állások száma
M[i] az i. ember által végezhető munkák száma
S[i,j] az i. ember által végezhető j. munka
ft(i,j)=igaz azonosan igaz függvény
fk(i,j,k,l)=(S[i,j]≠S[k,l]) nem végezhetnek azonos munkát
Itt is a két belső eljárást kell újrafogalmazni.
Jó_eset_keresés(M,X,I,mely,VAN):
mely:=X[I]+1
Ciklus amíg mely≤M[I] és Rossz_eset(I,X,mely)
mely:=mely+1
Ciklus vége
VAN:=(mely≤M[I])
Eljárás vége.
Rossz_eset(I,X,mely):
J:=1
Ciklus amíg J<I és S[J,X[J]]≠S[I,mely]
J:=J+1
Ciklus vége
Rossz_eset:=(J<I)
Eljárás vége.


A második változatban az emberek tudását egy mátrixban tároljuk, amelyben egy ember és egy munka sorszámához rendelünk igaz vagy hamis értéket aszerint, hogy az ember azt a munkát el tudja-e végezni vagy sem.
N az emberek és az állások száma
N az i. ember által végezhető munkák száma
S[i,j] az i. ember el tudja-e végezni a j. munkát
ft(i,j)=S[i,j]
fk(i,j,k,l)=(j≠l) nem végezhetnek azonos munkát
Megint a két belső eljárást fogalmazzuk újra.
Jó_eset_keresés(M,X,I,mely,VAN):
mely:=X[I]+1
Ciklus amíg mely≤M[I] és (Rossz_eset(I,X,mely) vagy
nem S[I,mely])
mely:=mely+1
Ciklus vége
VAN:=(mely≤M[I])
Eljárás vége.
Rossz_eset(I,X,mely):
J:=1
Ciklus amíg J<I és X[J]≠mely
J:=J+1
Ciklus vége
Rossz_eset:=(J<I)
Eljárás vége.


F39. N közért – M pékség
F39. N db közért M db pékségtől rendelhet kenyeret. Ismerjük a közértek kenyérigényét, a pékségek sütési kapacitását, valamint azt, hogy melyik közért mely pékségekkel áll kapcsolatban. Adjuk meg, hogy melyik közért melyik pékségtől rendelje a kenyeret, ha mindegyik csak egyetlentől rendelhet!
Tároljuk a közértek kenyérigényét, a pékségek sütési kapacitását, a közértek és a pékségek kapcsolatát!
N,M közértek száma, pékségek száma
IGENY[i] az i. közért kenyérigénye
KAPACITAS[j] a j. pékség sütési kapacitása
KAPCS[i,j] van-e kapcsolat az i. közért és a j. pékség között
ft(i,j)=KAPCS[i,j]
fk(i,X[i],X[1],...,X[i-1])=(SZUM(j=1..i, X[j]=X[i]) IGENY[j])≤KAPACITAS[X[i]]
Újra a két belső eljárást fogalmazzuk meg;
Jó_eset_keresés(M,X,I,mely,VAN):
mely:=X[I]+1
Ciklus amíg mely≤M[I] és (Rossz_eset(I,X,mely) vagy
nem KAPCS[I,mely])
mely:=mely+1
Ciklus vége
VAN:=(mely≤M[I])
Eljárás vége.
Rossz_eset(I,X,mely):
S:=0
Ciklus J=1-től I-ig
Ha X[I]=X[J] akkor S:=S+IGENY[J]
Ciklus vége
Rossz_eset:=(S>KAPACITAS[mely])
Eljárás vége.

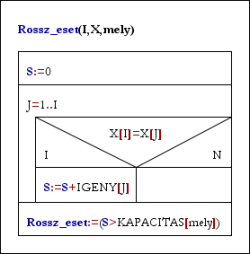
Elképzelhető, hogy e feladatnak nincs megoldása. Ekkor módosítsuk úgy a feladatot, hogy olyan megoldást adjunk, amelyben a lehető legtöbb közért kap kenyeret valamelyik pékségtől.
Ezt a – hiányos – megoldást úgy állítjuk elő, hogy felveszünk egy M+1 fiktív pékséget, amely tetszőleges mennyiségű kenyeret képes sütni, s akivel mindenki kapcsolatban van. Előállítjuk az összes megoldást, s azt választjuk ki közülük, amelyben a legtöbb olyan közért van, amely nem a fiktív szállítótól kapja a kenyeret. A költségfüggvényt kell definiálnunk:
kt(X)=SZUM(i=1..N) χ(X[i] ≠M+1), ahol χ(log) = {1, ha log; 0, ha nem log}
Programozási tételek backtrack-es változatainak mechanikus előállítása
A fejezet befejezéseként egy másik módszert is leírunk, amellyel némileg egyszerűbb megoldásokat lehet kreálni a backtrack-es tételvariánsokhoz. Egy apró észrevenni valóra építünk, amely után teljesen mechanikusan kaphatók meg az algoritmusok a már jól ismert alapvariánsaiból.
Induljunk ki a backtrack első algoritmusának legfelsőbb szintjéből, és hasonlítsuk össze a lineáris keresés tétel algoritmusával. Alighanem a következő analógiákat fedezzük föl:
Backtrack-es keresés → Lineáris keresés
I:=1 [komponens sorszám] → I:=1 [elemsorszám]
X[1..N]:=(0,...,0) [kezdőindexek]
I≥1 [van-e még keresnivaló] → I≤N [van-e még elem]
I≤N [van-e még megoldáskomponens] → T(X[I]) [T tul-e]
Jó_eset_keresés(I,mely,VAN) → I:=I+1 [köv. elem]
Ha VAN akkor X[I]:=mely; I:=I+1
különben X[I]:=0; I:=I-1
[a következő komponens]
Nézzük ez alapján pl. a kiválasztást!
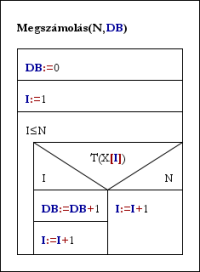
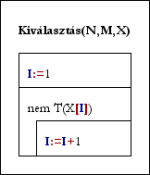
Kiválasztás(N,M,X): Kiválasztás(N,M,X):
I:=1; X[1..N]:=(0,...,0) I:=1
Ciklus amíg I≤N Ciklus amíg nem T(X[I])
Jó_eset_keresés(M,X,I,mely,VAN)
Ha VAN akkor X[I]:=mely; I:=I+1 I:=I+1
különben X[I]:=0; I:=I-1
Ciklus vége Ciklus vége
Eljárás vége. Eljárás vége.
A megszámolás és a kiválogatás tételek származtatásának egy látszólagos akadálya van. Nevezetesen az, hogy abban nem 'amíg'-os ciklus szerepel. Ezen azonban keresztül tudunk siklani azzal, ha átírjuk a számlálásos ciklust amíg-osra:
Ciklus I=1-től N-ig I:=1
Ciklus amíg I≤N
... ...
I:=I+1
Ciklus vége Ciklus vége
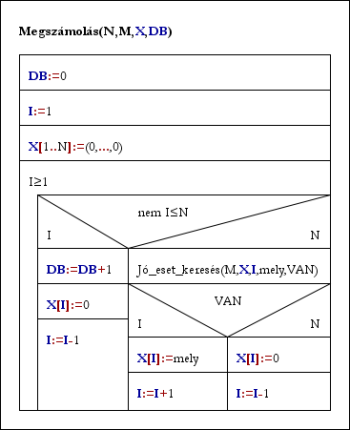
Az átírásnak most már semmi akadálya nincs. Pl. a megszámolásé az alábbi:
Megszámolás(N,M,X,DB): Megszámolás(N,DB):
DB:=0 DB:=0
I:=1; X[1..N]:=(0,...,0) I:=1
Ciklus amíg I≥1 Ciklus amíg I≤N
Ha nem I≤N akkor Ha T(X[I]) akkor
DB:=DB+1 DB:=DB+1
X[I]:=0; I:=I-1 I:=I+1
különben különben
Jó_eset_keresés(M,X,I,mely,VAN)
Ha VAN akkor X[I]:=mely; I:=I+1 I:=I+1
különben X[I]:=0; I:=I-1
Elágazás vége Elágazás vége
Ciklus vége Ciklus vége
Eljárás vége. Eljárás vége.